Расчёт надёжности k из n элементов с учетом конфигурации системы
Одной из интересных задач, которые встают перед инженером по надёжности - это расчёт надёжности системы, у которой из n элементов может отказать k.
Примеры подобных задач:
1. БШМ-К "Избушка" имеет в своём составе 4 генератора, заряжающие аккумуляторы от дизельного двигателя. Избушка сохраняет работоспособность при отказе 2 генераторов.

2. Парашютная система спускаемого аппарата для исследования потенциально обитаемой планеты состоит из 5 парашютов. Для обеспечения безопасной скорости снижения, при которой аппарат гарантированно не разобьётся, достаточно чтобы раскрылись 3 парашюта из 5. Значит 2 могут отказать.
3. Мультикоптер, несёт на борту 6 электродвигателей, вращающих 6 винтов. Он способен продолжать полёт при отказе 3 двигателей из 6.

Многие инженеры пасуют перед такой задачей, либо получают неверные результаты в результате расчётов. Одной из причин этого, на мой взгляд, является слабое знакомство с замечательной наукой о различных сочетаниях и комбинациях - комбинаторикой. Давайте посмотрим, как комбинаторика помогает делать изделия более надёжными.
Ещё более интересной задача становится, когда в системе из n элементов может отказать не просто k компонентов, а при определённом условии. Например, в крыле ударного беспилотника расположено 4 электропривода, управляющие 4 флаперонами (управляющая поверхность крыла самолёта, выполняющая одновременно функции элерона и закрылка). При этом из 4 электроприводов может отказать 2. Но отказы должны быть на разных консолях крыла, а не на одной, иначе БПЛА ждёт авария.

Другой пример: у упомянутого выше мультикоптера по-прежнему может отказать 3 электродвигателя из 6, при этом не все 3 правого или левого борта.
С этой задачей справляется ещё меньше людей, либо просто её не рассматривает. Давайте научимся считать вероятность отказа в таких ситуациях!
Рассмотрим ситуацию, когда в системе, состоящей из 4 элементов может отказать 2 любых элемента.
Подумаем, какие события будут удовлетворять нашим условиям?
1 событие. При работе системы не возникло ни одного отказа - нам это подходит.
2 событие. При работе системы возник 1 отказ - тоже подходит.
3 событие. При работе системы возникло 2 отказа - и это подходит.
Вероятность возникновения первого события определим по формуле:

С – число возможных отказных ситуаций, определяется по формуле из комбинаторики, число сочетаний без возвращения.
Число сочетаний без возвращения:

n – общее число элементов системы
k – число отказавших элементов
P – вероятность безотказной работы 1 элемента за время t. Определяется по следующей формуле:

λ – интенсивность отказов элемента
t – время работы
Q – вероятность отказа 1 элемента за время t. Определяется по следующей формуле:

Вероятность возникновения второго события (при работе системы возник 1 отказ) определим по формуле:

Вероятность возникновения третьего события (при работе системы возникло 2 отказа) определим по формуле:

Вероятность безотказной работы системы, состоящей из 4 элементов при двух возможных отказах определим по формуле:

Чтобы проверить правильность своих рассуждений, рассчитаем вероятность оставшихся событий:


Проверим сами себя. Полная группа событий (сумма вероятностей всех возможных исходов) определится по формуле:

Посчитаем реальный пример. Пусть система управления БПЛА состоит из 4 электроприводов в крыле. При этом из них может отказать 2 любых привода. Пока не будем учитывать, что отказы могут быть только на разных консолях крыла.

Пусть из интенсивность отказов электропривода λ составляет:

Пусть время полёта ударного БПЛА составляет 10 часов.
Тогда ВБР (вероятность безотказной работы) электропривода по формуле (3):

Вероятность отказа по формуле (4):

Число возможных ситуаций при 0 отказов по формуле (2). Думаю понятно, что если у нас не было отказов, то у нас есть только 1 ситуация.
Значит

Чтобы быстро считать число комбинаций, рекомендую использовать в экселе формулу =COMBIN(1;2)
или =ЧИСЛОКОМБ(1;2) в русскоязычном экселе. 1 - общее число элементов, 2 - число отказавших элементов.
Ну что, посчитаем вероятность 1 события. При работе системы не возникло ни одного отказа.

Аналогично посчитаем вероятности следующих событий:
При работе системы возник 1 отказ.

При работе системы возникло 2 отказа.

Посчитаем теперь ВБР системы, состоящей из 4 элементов при 2 возможных отказах определим по формуле:

ВБР системы получилась достаточно высокой!
Теперь усложним задачу. Тот же самый БПЛА. Снова 4 электропривода и снова 2 возможных отказа. Но теперь возможно только по 1 отказу на каждой консоле крыла. Если произойдут 2 одновременных отказа на правой или левой консоли, БИУС (бортовая информационная управляющая система) сойдет с ума и разобьёт беспилотник.
Давайте посчитаем, сколько возможно отказных ситуаций при 2 отказах из 4 электроприводов.
Вспомним формулу (2)

Посмотрим на картинку.
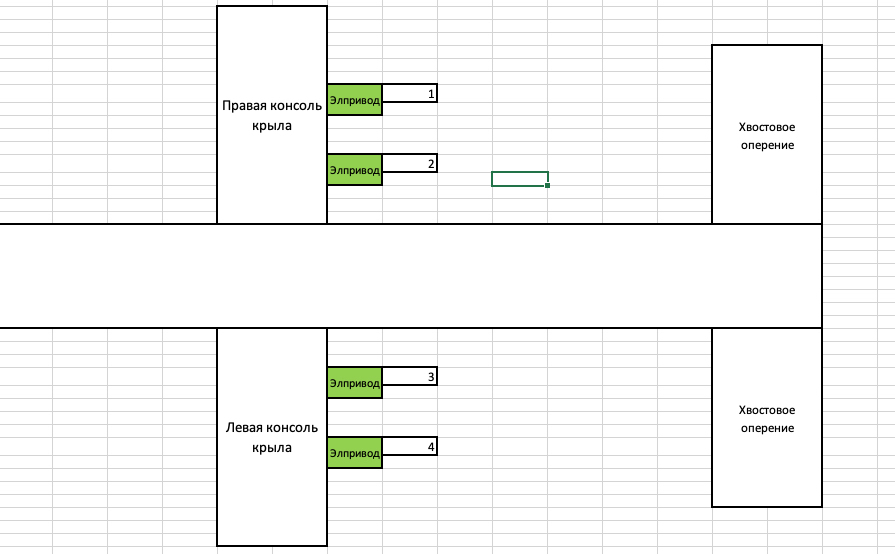
1. Отказ привода №1 и № 2. - Нас эта ситуация не устраивает, они на одной консоли.
2. Отказ привода №1 и № 3. - Устраивает. Они на разных консолях.
3. Отказ привода №1 и № 4. - Устраивает. Они на разных консолях.
4. Отказ привода №2 и № 3. - Устраивает. Они на разных консолях.
5. Отказ привода №2 и № 4. - Устраивает. Они на разных консолях.
6. Отказ привода №3 и № 4. - Нас эта ситуация не устраивает, они на одной консоли.
Таким образом, из 6 ситуаций при 2 отказах из 4 электроприводов, нас устраивает 4 из 6 ситуаций. Каким образом мы используем эту информацию?
Вспомним формулу, которую мы использовали для расчёта вероятности возникновения 2 отказов из 4 электроприводов:

Чтобы правильно посчитать интересующую нас ситуацию, нам необходимо чтобы одновременно произошли 2 события: отказали 2 электропривода и эти электроприводы были на разных консолях крыла.
Вспомним, что по классической теории вероятностей, вероятность одновременно наступления двух событий:

Думаю, что вы догадались, что

Тогда формула для события отказ двух электроприводов на разных консолях крыла будет выглядеть следующим образом:

Ну и наконец, посчитаем ВБР системы, состоящей из 4 элементов при 2 возможных отказах, но на разных консолях крыла:

Сравним это с тем, что у нас получилось для ВБР без учета стороны крыла: 0,9999999997.
Как видим, надёжность стала меньше, но это подтверждает, что мы посчитали верно. Лучше получить меньшее число, заранее, на этапе разработки принять меры для повышения надёжности, чем получить неверное, но большое число, успокоиться, получить отказ электроприводов при испытаниях, рвать себе волосы на одном месте, тратить кучу денег в времени.
В завершение предлагаю вам мой удобный калькулятор для расчётов k из n. И мою другую статью, рассказывающую как комбинаторика помогает нам сохранять наши личные данные и деньги.
Пусть ваша техника будет надёжной! Инженер по надёжности, Алексей Глазачев.





